 Divulgación matemática
Divulgación matemática
Ya sea como simples juegos de entretenimiento o ejercicios en textos escolares, las secuencias numéricas permiten adentrarnos tímidamente en las profundidades de la aritmética. Algunas de ellas son fuente de intenso estudio en la matemática actual. Otras, más conocidas, se nos aparecen cotidianamente, pues son usadas, por ejemplo, en la industria del diseño.
Completar secuencias numéricas puede ser un pasatiempo divertido. Es por ello que problemas de este tipo suelen hallarse no solo en textos escolares, sino también en secciones de entretenimiento de diarios y revistas, así como en muchos sitios de internet (para confirmar esto, basta realizar una búsqueda con la frase “qué número sigue”).
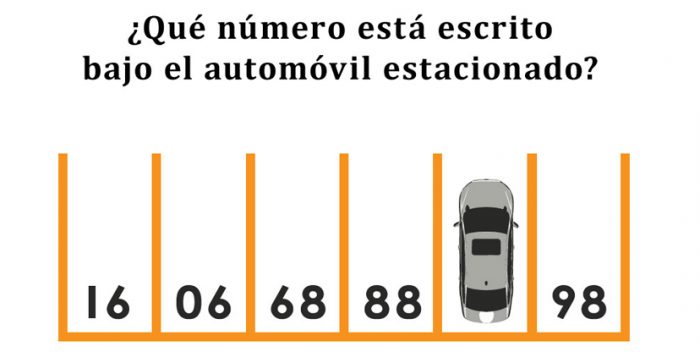
Mi favorito, ilustrado en la imagen principal, fue incluido hace algunos años en el examen de admisión a un colegio de Hong Kong. Sorprendentemente, los adultos que quisieron resolverlo tuvieron –en promedio– un desempeño menos satisfactorio. La razón apuntaría a que, como los niños no tienen un conocimiento tan estructurado, se dieron una mayor libertad intelectual para lidiar con él, lo que les permitió resolverlo de la manera más sencilla que pueda imaginarse. De hecho, son precisamente los niños quienes suelen disfrutar más con este tipo de desafíos intelectuales. Para ellos, se trata de simples juegos, y difícilmente sospechan que en el intento de encontrar su solución se adentran tímidamente en las profundidades de la aritmética. (Si voltea el dibujo en 180 grados, la solución le será evidente. Por cierto, la sucesión 2, 10, 12, 16, 17, 18,19, … también tiene una regla curiosa: los números listados son aquellos que comienzan con la letra “d”, por lo que el siguiente es el 200.)
Siendo matemáticamente quisquillosos, debemos señalar que, en estricto rigor, todos estos acertijos están mal formulados. La razón de esto radica en que las reglas que se adecuan a los elementos de una secuencia nunca son únicas.
De hecho, si usted completa una secuencia de la manera que se le antoje, siempre es posible elucubrar una regla que se ajuste a su elección. Para clarificar un poco esto, consideremos la secuencia 1, 2, 4, 8, 16,… ¿Cuál número sigue? La tentación es obvia: 32. Sin embargo, podría perfectamente seguir el 31, el 2016, el 666 o el 24.500-03.
En efecto, para cada una de las secuencias así formadas existe una regla traducible en una fórmula polinomial de grado menor que la cantidad de datos (en este caso, menor que 5). Así nos lo indica una receta ideada por el célebre matemático franco-italiano del siglo XVIII Joseph-Louis Lagrange, comúnmente conocida como la “interpolación de Lagrange”. Por ejemplo, si usted completa la secuencia con un 31, esta receta nos entrega el polinomio
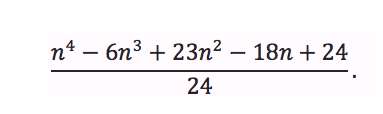
La comprobación es una mera cuestión de cálculo:

Si bien todo esto puede parecer un poco artificial, hay ocasiones en que estas secuencias inesperadas surgen naturalmente. Consideremos, por ejemplo, la siguiente situación: si se escoge una cantidad de vértices sobre una circunferencia y se dibujan todos los trazos que unan pares de estos vértices, ¿en cuántas regiones puede, a lo máximo, quedar dividido el círculo? Ciertamente, el número máximo se obtendrá cuando la posición de los vértices sea tal que no haya tres trazos que pasen por el mismo punto.
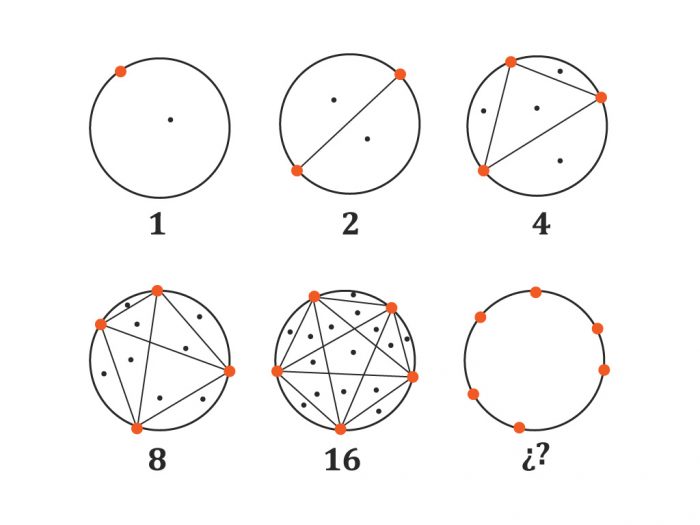
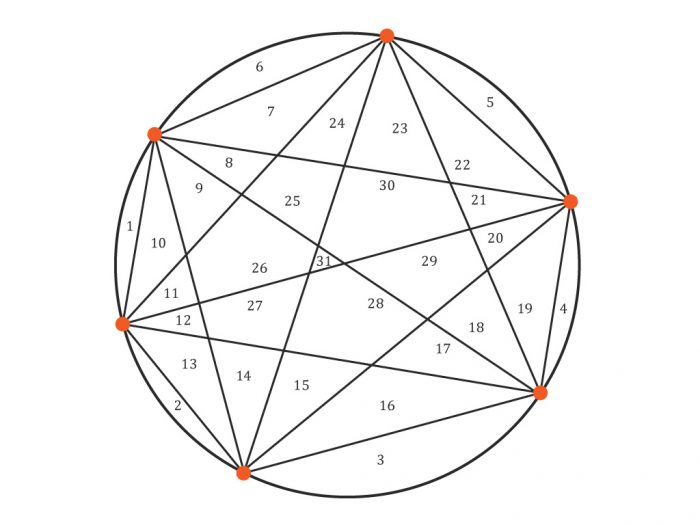
Para una cantidad de vértices igual a 1, 2, 3, 4 y 5, el número de regiones es, respectivamente, 1, 2, 4, 8 y 16. Sin embargo, al escoger 6 vértices, la cantidad máxima de regiones es… ¡31! De hecho, la complicada fórmula polinomial dada más arriba corresponde exactamente al número máximo de regiones que aparecen al escoger una cantidad n de vértices y dibujar los trazos correspondientes (aunque esto está lejos de ser evidente; es más, su prueba es bastante elaborada).
Más allá de juegos y curiosidades, la ciencia matemática está repleta de secuencias numéricas de enorme interés (y perfectamente definidas por medio de reglas claras). De hecho, hay tantas secuencias interesantes que, después de haber escrito dos libros de recopilación, el matemático británico Neil Sloane decidió crear un repositorio virtual, el Online Encyclopedia of Integer Sequences (OEIS).
Al mes de agosto de 2015, este contenía nada menos que 260 mil secuencias, cada una con el nombre de su descubridor y una breve reseña de sus propiedades y la justificación de su relevancia. Algunas de ellas son aún fuente de intenso estudio, y están lejos de ser completamente entendidas. A modo de ilustración, me referiré brevemente solo a la más famosa, indexada como la OEIS A000045. Esta empieza con los números
y su regla de formación es muy sencilla: comenzando con dos cifras iguales a 1, a partir del tercer término, cada elemento es igual a la suma de los dos anteriores. Por ejemplo:
Aunque esta secuencia aparece en textos hindúes que datan del siglo II a.C., su descubrimiento es generalmente datado en el siglo XI d.C. y atribuido al italiano Leonardo de Pisa, más conocido por su apodo: Fibonacci. El interés de este matemático por esta secuencia se originó de un modelo sencillo que buscaba entender el crecimiento de una población de conejos, aunque se aplica de manera más nítida al estudio de los árboles genealógicos de las abejas.
En efecto, como los machos (zánganos) no tienen padre y las hembras tienen padre y madre, dicho árbol es bastante peculiar: si observa con atención, notará que el número de ascendientes en cada generación corresponde a un término entre 1, 1, 2, 3, 5, 8, 13, …
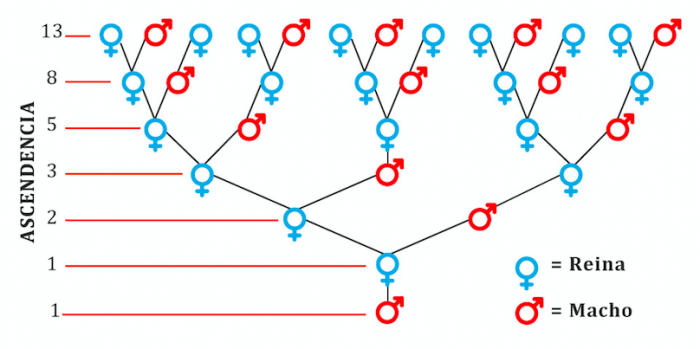
La secuencia de Fibonacci está relacionada con muchísimos procesos naturales. Solo por mencionar uno, busque una flor cercana y cuente su número de pétalos: se sorprenderá al constatar que, muy probablemente, dicho número aparece en la secuencia.
 De hecho, casi con total certeza, este será el caso si usted escogió una margarita. Así, con este dato en mente, puede conocer el resultado del tierno y desesperante “me quiere / no me quiere” jugado con esta flor sin necesidad de arrancarle los pétalos. Por cierto, dado que en la secuencia se suceden dos números impares por cada par, es más probable que sus sentimientos sean correspondidos. “El amor es más fuerte”, diría Fibonacci…
De hecho, casi con total certeza, este será el caso si usted escogió una margarita. Así, con este dato en mente, puede conocer el resultado del tierno y desesperante “me quiere / no me quiere” jugado con esta flor sin necesidad de arrancarle los pétalos. Por cierto, dado que en la secuencia se suceden dos números impares por cada par, es más probable que sus sentimientos sean correspondidos. “El amor es más fuerte”, diría Fibonacci…

Otro aspecto interesante de la secuencia es su relación con la división áurea (la misma que aparece en nuestra bandera de la Independencia; vea la nota aquí). En efecto, los cocientes entre los términos sucesivos se aproximan más y más al número de oro
tal como se observa a continuación:
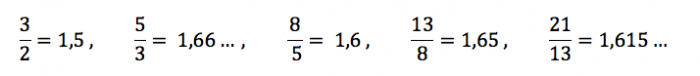
Esto queda corroborado por la sorprendente fórmula descubierta (recién en el siglo XIX) por el francés Édouard Lucas para el término que aparece en la posición n-ésima: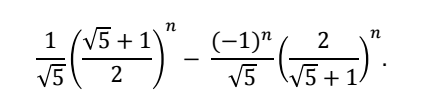
En fin, dadas todas sus propiedades, no resulta extraño que hasta el día de hoy esta secuencia siga maravillando a matemáticos de todo el mundo. De hecho, es tal el nivel de fascinación que una revista especializada, The Fibonacci Quarterly, solo publica artículos de investigación que tienen alguna relación con ella.
Es más, dicha revista surgió al alero de una organización mundial, la Fibonacci Association, que por estos días celebra, en Caen (Francia), nada menos que el Décimo-Séptimo Congreso Internacional sobre Números de Fibonacci y sus Aplicaciones: http://www.math.unicaen.fr/fibonacci/.
Si quiere seguir disfrutando de las maravillas de esta cadena de números, le recomiendo este bello documental o, si dispone de un poco menos de tiempo, esta breve charla TED de Arthur Benjamin. Ahora bien, si todo esto le resulta indiferente y piensa que nunca más en su vida verá esta secuencia, lamento informarle que es muy probable que la tenga frente a usted cotidianamente. Incluso, puede que en este mismo instante sus proporciones estén secretamente desplegadas en la pantalla de su computador o teléfono celular. Solo observe con atención:
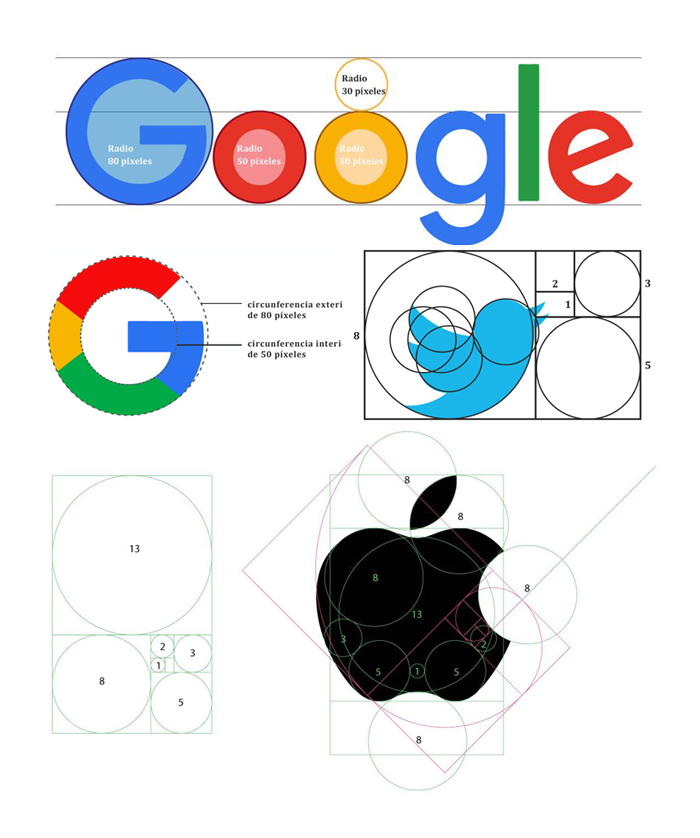
Si bien las especificidades métricas de estos logotipos son materia de debate en internet, claramente están inspiradas en la secuencia de Fibonacci y su relación con la división áurea. De hecho, estas son frecuentemente utilizadas en trabajos de diseño.